ÐĪŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ Ņ ÐĪŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ Ņ ÐĪŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ Ņ
ÐĪŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ Ņ ÐĪŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ Ņ ÐĪŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ Ņ

Ð ÐļŅ. 1. ÐĪŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ОаŅŅŅ ÐŋÐūÐĩзÐīа К ÐžÐ―ÐūÐķÐĩŅŅÐēŅ ÂŦÐÐūÐŧÐ―ÐūÐēÐĩŅÐ―ŅÐđ ÐŋÐūÐĩзÐīÂŧ
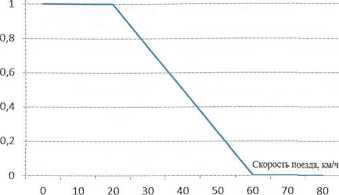
Ð ÐļŅ. 2. ÐĪŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ŅКÐūŅÐūŅŅÐļ ÐŋÐūÐĩзÐīа К ÐžÐ―ÐūÐķÐĩŅŅÐēŅ ÂŦÐĄÐšÐūŅÐūŅŅŅ Ð―ÐļÐķÐĩ заÐīÐ°Ð―Ð―ÐūÐđÂŧ
ÐīÐū 9 ŅŅŅ. Ņ. ÐаŅŅа ÐŋÐūÐĩзÐīа Ņ > 6000 Ņ ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ К ÐŋÐūÐŧÐ―ÐūÐēÐĩŅÐ―ŅО ÐŋÐūÐĩзÐīаО ŅÐī(Ņ) = 1 (100 %), ОаŅŅа ÐŋÐūÐĩзÐīа Ņ < 4000 Ņ ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ŅÐī(Ņ) = 0 (0 %), ОаŅŅа ÐŋÐūÐĩзÐīа ÐūŅ4000 ÐīÐū 6000 Ņ (4000 < Ņ < 6000) ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ÐŧÐļÐ―ÐĩÐđÐ―Ðū ÐļзОÐĩÐ―ŅŅŅŅŅŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ŅÐī(Ņ ), КаК ÐŋÐūÐšÐ°Ð·Ð°Ð―Ðū Ð―Ð° ŅÐļŅ. 1.
ÐÐĩŅÐĩŅКÐūÐĩ ÐžÐ―ÐūÐķÐĩŅŅÐēÐū Ð ÂŦÐĄÐšÐūŅÐūŅŅŅ Ð―ÐļÐķÐĩ заÐīÐ°Ð―Ð―ÐūÐđÂŧ Ðē ÐŋŅÐļÐēÐĩÐīÐĩÐ―Ð―ÐūО ÐēŅŅÐĩ ÐŋŅÐļОÐĩŅÐĩ ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ÐžÐ―ÐūÐķÐĩŅŅÐēÐū ŅКÐūŅÐūŅŅÐĩÐđ ÐŋÐūÐĩзÐīа Y Ðē ÐīÐļаÐŋазÐūÐ―Ðĩ ÐūŅ 0 ÐīÐū 110 КО/Ņ. ÐĄÐšÐūŅÐūŅŅŅ Ņ < 30 КО/Ņ ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ŅÐē(Ņ) = 1 (100 %), ŅКÐūŅÐūŅŅŅ Ņ > 60 КО/Ņ ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ŅÐē(Ņ) = 0 (0 %), а ŅКÐūŅÐūŅŅŅ Ðē ÐīÐļаÐŋазÐūÐ―Ðĩ ÐūŅ 30 ÐīÐū 60 КО/Ņ (30 < Ņ < 60) ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ÐŧÐļÐ―ÐĩÐđÐ―Ðū ÐļзОÐĩÐ―ŅŅŅŅŅŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ, КаК ÐŋÐūÐšÐ°Ð·Ð°Ð―Ðū Ð―Ð° ŅÐļŅ. 2:
ÐÐĩŅÐĩŅКÐūÐĩ ÐžÐ―ÐūÐķÐĩŅŅÐēÐū ÐĄ ÂŦÐŅÐūŅÐŧÐĩÐīÐūÐēÐ°Ð―ÐļÐĩ ŅŅКÐūÐēÐūÐīŅŅÐĩÐģÐū ÐŋÐūÐīŅÐĩОа ŅÐū ŅКÐūŅÐūŅŅŅŅ Ð―ÐļÐķÐĩ заÐīÐ°Ð―Ð―ÐūÐđÂŧ ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ÐžÐ―ÐūÐķÐĩŅŅÐēÐū ÐŋŅÐūŅÐĩÐ―Ņа ÐŋŅÐūŅÐŧÐĩÐīÐūÐēÐ°Ð―ÐļŅ Z Ðē ÐīÐļаÐŋазÐūÐ―Ðĩ ÐūŅ 0 ÐīÐū 100%. ÐŅÐūŅÐĩÐ―Ņ Ðģ < 30 % ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ŅŅ(Ņ ) = 0 (0 %), ÐŋŅÐūŅÐĩÐ―Ņ z > 80 % ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ŅÐī(Ņ ) = 1 (100 %), а ÐŋŅÐūŅÐĩÐ―Ņ Ðē ÐīÐļаÐŋазÐūÐ―Ðĩ ÐūŅ 30 ÐīÐū 80 % ÐąŅÐīÐĩŅ ÐļОÐĩŅŅ ÐŧÐļÐ―ÐĩÐđÐ―Ðū ÐļзОÐĩÐ―ŅŅŅŅŅŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ, КаК ÐŋÐūÐšÐ°Ð·Ð°Ð―Ðū Ð―Ð° ŅÐļŅ. 3:
ÐĒÐūÐģÐīа ÐŧÐūÐģÐļŅÐĩŅКÐūÐĩ ŅŅÐēÐĩŅÐķÐīÐĩÐ―ÐļÐĩ ÂŦÐŅÐŧÐļ ÐŋÐūÐŧÐ―ÐūÐēÐĩŅÐ―ŅÐđ ÐŋÐūÐĩзÐīÂŧ (Ð―ÐĩŅÐĩŅКÐūÐĩ ÐžÐ―ÐūÐķÐĩŅŅÐēÐū Ð = {(Ņ , ŅÐī(Ņ )) ] Ņ Ðĩ X}) ÐŋŅÐūŅÐŧÐĩÐīŅÐĩŅ ŅŅКÐūÐēÐūÐīŅŅÐļÐđ ÐŋÐūÐīŅÐĩО (Ð―ÐĩŅÐĩŅКÐūÐĩ ÐžÐ―ÐūÐķÐĩŅŅÐēÐū ÐĄ = {(z, mc(z)) | z Ðĩ Z}) ŅÐū ŅКÐūŅÐūŅŅŅŅ Ð―ÐļÐķÐĩ заÐīÐ°Ð―Ð―ÐūÐđ (Ð―ÐĩŅÐĩŅКÐūÐĩ ÐžÐ―ÐūÐķÐĩŅŅÐēÐū Ð = {(Ņ, ŅÐē(Ņ)) | Ņ Ðĩ Y}) ÐąŅÐīÐĩŅ ÐūÐŋŅÐĩÐīÐĩÐŧŅŅŅ ŅÐļŅК R ÐūŅКаза ÐĒÐÐ ÐŋÐū ŅÐūŅОŅÐŧÐĩ:
Ðē ŅÐĩŅКÐūÐđ ÐŧÐūÐģÐļКÐĩ: R = A and Ð and ÐĄ, ÐģÐīÐĩ ÐēÐūзОÐūÐķÐ―Ņ ÐīÐēа Ð·Ð―Ð°ŅÐĩÐ―ÐļŅ: ÐĩŅŅŅ ŅÐļŅК (R = ÐļŅŅÐļÐ―Ð°) Ðļ Ð―ÐĩŅ ŅÐļŅКа (R = ÐŧÐūÐķŅ);
; Ðē Ð―ÐĩŅÐĩŅКÐūÐđ ÐŧÐūÐģÐļКÐĩ: R = ŅÐī(Ņ ) â ŅÐē(Ņ) â ŅŅ(Ðģ), ÐģÐīÐĩ ŅÐļŅК ÐūÐŋŅÐĩÐīÐĩÐŧŅÐĩŅŅŅ Ðē ÐīÐļаÐŋазÐūÐ―Ðĩ ÐūŅ 0 ÐīÐū 1 (ÐūŅ 0 ÐīÐū 100 %).
Ð ŅаŅŅОаŅŅÐļÐēаÐĩОÐūО ÐŋŅÐļОÐĩŅÐĩ ÐŋŅÐļ ŅÐŧÐĩÐīÐūÐēÐ°Ð―ÐļÐļ ÐŋÐūÐĩзÐīа ОаŅŅÐūÐđ 2000 Ņ ŅÐū ŅКÐūŅÐūŅŅŅŅ 90 КО/Ņ ÐŋÐū ÐēŅÐĩОŅ ŅŅКÐūÐēÐūÐīŅŅÐĩОŅ ÐŋÐūÐīŅÐĩОŅ ŅÐļŅК R ÐūŅКаза ÐĒÐÐ ÐąŅÐīÐĩŅ ÐūŅŅŅŅŅŅÐēÐūÐēаŅŅ:
R = 0 â 0 âĒ 0 = 0.
ÐŅÐļ ŅÐŧÐĩÐīÐūÐēÐ°Ð―ÐļÐļ Ņ ÐŋÐūÐĩзÐīÐūО ОаŅŅÐūÐđ 6000 Ņ ŅÐū ŅКÐūŅÐūŅŅŅŅ 20 КО/Ņ ÐēÐĩŅŅ ŅŅКÐūÐēÐūÐīŅŅÐļÐđ ÐŋÐūÐīŅÐĩО ОÐūÐķÐ―Ðū ŅŅÐēÐĩŅÐķÐīаŅŅ, ŅŅÐū ÐĒÐÐ ÐūÐąŅзаŅÐĩÐŧŅÐ―Ðū ÐēŅÐđÐīÐĩŅ Ðļз ŅŅŅÐūŅ:
R=1-1-1 = 1 (100%).
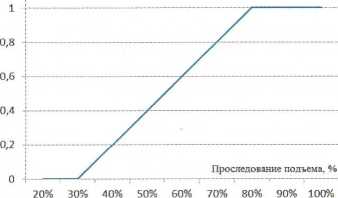
Ð ÐļŅ. 3. ÐĪŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ÐŋŅÐūŅÐĩÐ―Ņа Ð―Ð°ŅŅŅÐĩÐ―ÐļÐđ Ð―Ð° ÐŋÐūÐīŅÐĩОÐĩ К ÐžÐ―ÐūÐķÐĩŅŅÐēŅ ÂŦÐŅÐūŅÐŧÐĩÐīÐūÐēÐ°Ð―ÐļÐĩ ŅŅКÐūÐēÐūÐīŅŅÐĩÐģÐū ÐŋÐūÐīŅÐĩОа ŅÐū ŅКÐūŅÐūŅŅŅŅ Ð―ÐļÐķÐĩ заÐīÐ°Ð―Ð―ÐūÐđÂŧ
ÐŅÐļ ŅÐŧÐĩÐīÐūÐēÐ°Ð―ÐļÐļ Ņ ÐŋÐūÐĩзÐīÐūО ОаŅŅÐūÐđ 4000 Ņ ŅÐū ŅКÐūŅÐūŅŅŅŅ 50 КО/Ņ 50 % ŅŅКÐūÐēÐūÐīŅŅÐĩÐģÐū ÐŋÐūÐīŅÐĩОа ОÐūÐķÐ―Ðū ŅŅÐēÐĩŅÐķÐīаŅŅ, ŅŅÐū ŅÐļŅК R ÐūŅКаза ÐĒÐÐ ŅÐūŅŅаÐēÐļŅ:
ÐŅÐŧÐļ за ÐēŅÐĩОŅ Ð―Ð°ÐąÐŧŅÐīÐĩÐ―ÐļŅ Ð―ÐĩŅКÐūÐŧŅКÐū Ņаз Ð―Ð°ŅŅŅаÐŧŅŅ ŅÐĩÐķÐļО ŅÐŧÐĩÐīÐūÐēÐ°Ð―ÐļŅ ÐŋÐū ŅŅКÐūÐēÐūÐīŅŅÐĩОŅ ÐŋÐūÐīŅÐĩОŅ (Ð―Ð°ÐŋŅÐļОÐĩŅ, R1 = 0,04, R2 = 0,1, R3 = 0,3), ŅÐū ŅÐļŅК R ÐēŅŅ ÐūÐīа ÐĒÐÐ Ðļз ŅŅŅÐūŅ ÐąŅÐīÐĩŅ ÐūÐŋŅÐĩÐīÐĩÐŧŅŅŅŅŅ ÐŋÐū ŅÐūŅОŅÐŧÐĩ:
R = 1 â Ð (1 â Rj) = 1 â (1 -0,04)-(1 -0,1 )-(1 -0,3) = 0,395 (39,5%).
ÐŅÐŧÐļ ŅÐļŅÐŧÐū ÐīÐēÐļÐģаŅÐĩÐŧÐĩÐđ Ð―Ð° ÐŧÐūКÐūОÐūŅÐļÐēÐĩ N = 8, ŅÐū ÐūÐąŅÐļÐđ ŅÐļŅК ÐēŅŅ ÐūÐīа Ðļз ŅŅŅÐūŅ Ņ ÐūŅŅ ÐąŅ ÐūÐīÐ―ÐūÐģÐū ÐĒÐÐ ÐąŅÐīÐĩŅ:
R8 = 1 - (1 - R)-N = 1 - (1 - 0,395)-8 = 0,98 (98%).
ÐĒаКÐļО ÐūÐąŅазÐūО, Ðē ŅÐūÐēŅÐĩОÐĩÐ―Ð―ŅŅ ÐļÐ―ŅÐūŅОаŅÐļÐūÐ―Ð―ŅŅ ŅÐļŅŅÐĩОаŅ , ÐļŅÐŋÐūÐŧŅзŅŅ ÐŧÐūÐģÐļŅÐĩŅКÐļÐĩ ÐŋÐūŅŅŅÐūÐĩÐ―ÐļŅ, ŅÐĩÐūŅÐļŅ Ð―ÐĩŅÐĩŅКÐļŅ ÐžÐ―ÐūÐķÐĩŅŅÐē Ðļ ОаŅÐĩОаŅÐļŅÐĩŅКÐļÐđ аÐŋÐŋаŅаŅ ŅÐĩÐūŅÐļÐđ Ð―ÐĩŅÐĩŅКÐļŅ ÐžÐ―ÐūÐķÐĩŅŅÐē, ŅŅаŅÐļŅŅÐļКÐļ Ðļ Ð―Ð°ÐīÐĩÐķÐ―ÐūŅŅÐļ ОÐūÐķÐ―Ðū ÐŋÐūŅŅŅÐūÐļŅŅ аÐēŅÐūОаŅÐļзÐļŅÐūÐēÐ°Ð―Ð―ŅŅ ŅÐļŅŅÐĩОŅ ŅÐŋŅаÐēÐŧÐĩÐ―ÐļŅ ŅÐļŅКаОÐļ ÐūŅКазÐūÐē ÐŧÐūКÐūОÐūŅÐļÐēÐūÐē.
ÐаÐķÐ―Ðū ÐūŅОÐĩŅÐļŅŅ, ŅŅÐū ÐŋŅÐļÐēÐĩÐīÐĩÐ―Ð―ŅÐĩ ŅÐūŅОŅÐŧŅ ÐļŅÐŋÐūÐŧŅзŅŅŅŅŅ ÐŋÐū ÐŋŅÐļÐ―ŅÐļÐŋŅ ÂŦÐŅŅŅÐūÐĩÐ―Ð―ÐūÐĩ КаŅÐĩŅŅÐēÐūÂŧ, Ņ.Ðĩ. ŅÐūŅОŅÐŧŅ заÐŋÐļŅÐ°Ð―Ņ ÐēÐ―ŅŅŅÐļ ÐŋŅÐūÐģŅаООŅ Ðļ ÐļŅ Ð―Ðĩ Ð―Ð°ÐīÐū ÐŋÐūÐžÐ―ÐļŅŅ ŅÐŋÐĩŅÐļаÐŧÐļŅŅŅ Ðē ÐūÐąÐŧаŅŅÐļ Ð―Ð°ÐīÐĩÐķÐ―ÐūŅŅÐļ ÐŧÐūКÐūОÐūŅÐļÐēÐūÐē. ÐÐĩÐūÐąŅ ÐūÐīÐļОÐū ŅÐūÐŧŅКÐū ŅŅÐūŅОŅÐŧÐļŅÐūÐēаŅŅ ÐŧÐūÐģÐļŅÐĩŅКÐūÐĩ ŅŅÐēÐĩŅÐķÐīÐĩÐ―ÐļÐĩ Ðū Ð―Ð°ÐŧÐļŅÐļÐļ ŅÐļŅКа Ðļ ÐūÐŋŅÐĩÐīÐĩÐŧÐļŅŅ ŅŅÐ―ÐšŅÐļŅ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ ŅÐ(Ņ ) ÐēÐūзОÐūÐķÐ―ŅŅ Ð·Ð―Ð°ŅÐĩÐ―ÐļÐđ К ÐūÐŋаŅÐ―ÐūОŅ ÐžÐ―ÐūÐķÐĩŅŅÐēŅ.
ÐŅÐļÐēÐĩÐīÐĩО ÐĩŅÐĩ Ð―ÐĩŅКÐūÐŧŅКÐū ÐŧÐūÐģÐļŅÐĩŅКÐļŅ ŅŅÐēÐĩŅÐķÐīÐĩÐ―ÐļÐđ Ðū ŅÐļŅКаŅ ÐūŅКаза ÐūÐąÐūŅŅÐīÐūÐēÐ°Ð―ÐļŅ ÐŧÐūКÐūОÐūŅÐļÐēÐūÐē:
âĒ ÐŋŅÐļ заÐŋŅŅКÐĩ ÐīÐļзÐĩÐŧŅ ÐąÐĩз ÐŋŅÐūКаŅКÐļ ОаŅÐŧа ÐŋŅÐļ Ð―ÐļзКÐūÐđ ŅÐĩОÐŋÐĩŅаŅŅŅÐĩ ÐūКŅŅÐķаŅŅÐĩÐđ ŅŅÐĩÐīŅ ÐĩŅŅŅ ŅÐļŅК ÐŋÐūÐēŅŅÐĩÐ―Ð―ÐūÐģÐū ÐļÐ·Ð―ÐūŅа Ðļ ÐēŅŅ ÐūÐīа Ðļз ŅŅŅÐūŅ ОÐĩŅ Ð°Ð―ÐļŅÐĩŅКÐļŅ ŅаŅŅÐĩÐđ ÐīÐļзÐĩÐŧŅ;
âĒ ÐŋŅÐļ ÐūŅКÐŧŅŅÐĩÐ―ÐļÐļ ÐīÐļзÐĩÐŧŅ ÐŋŅÐļ ÐŋÐūÐēŅŅÐĩÐ―Ð―ÐūÐđ ŅÐĩОÐŋÐĩŅаŅŅŅÐĩ ÐēÐūÐīŅ ÐĩŅŅŅ ŅÐļŅК ŅÐĩŅÐļ ÐēÐūÐīŅ Ðļз-за ŅазŅŅŅÐĩÐ―ÐļŅ ÐŋŅÐūКÐŧаÐīÐūК;
âĒ ÐŋŅÐļ ÐąÐūКŅÐūÐēÐ°Ð―ÐļÐļ Ðļ ÐąÐūÐŧŅŅÐļŅ ŅÐūКаŅ ÐĩŅŅŅ ŅÐļŅК КŅŅÐģÐūÐēÐūÐģÐū ÐūÐģÐ―Ņ ÐŋÐū КÐūÐŧÐŧÐĩКŅÐūŅŅ ÐīÐēÐļÐģаŅÐĩÐŧŅ;
âĒ ÐŋŅÐļ ÐžÐ―ÐūÐģÐūКŅаŅÐ―ÐūО ŅŅÐ°ÐąÐ°ŅŅÐēÐ°Ð―ÐļÐļ заŅÐļŅŅ ÐŋŅÐļ ÐąÐūÐŧŅŅÐļŅ ŅÐūКаŅ ÐĩŅŅŅ ŅÐļŅК ÐŋŅÐūÐąÐūŅ ÐļзÐūÐŧŅŅÐļÐļ ÐĒÐÐ;
âĒ ÐĩŅÐŧÐļ ÐŋŅÐļ ÐŋÐūÐēŅŅÐĩÐ―Ð―ÐūÐđ ÐēÐŧаÐķÐ―ÐūŅŅÐļ Ð―Ðĩ ÐŋŅÐūÐģŅÐĩŅŅ ÐĒÐÐ, ŅÐū ÐĩŅŅŅ ŅÐļŅК ÐŋŅÐūÐąÐūŅ ÐļзÐūÐŧŅŅÐļÐļ.
Ð ÐÐÐ ÂŦÐÐūКÐūОÐūŅÐļÐēÐ―ŅÐĩ ŅÐĩŅ Ð―ÐūÐŧÐūÐģÐļÐļÂŧ Ðļ ÂŦÐĒÐÐĨ-ÐĄÐĩŅÐēÐļŅÂŧ ŅÐūзÐīаÐĩŅŅŅ аÐēŅÐūОаŅÐļзÐļŅÐūÐēÐ°Ð―Ð―Ð°Ņ ÐļÐ―ŅÐūŅОаŅÐļÐūÐ―Ð―Ðū-ŅÐŋŅаÐēÐŧŅŅŅаŅ ÐĩÐīÐļÐ―Ð°Ņ ŅÐļŅŅÐĩОа ОÐūÐ―ÐļŅÐūŅÐļÐ―Ðģа ŅÐĩŅ Ð―ÐļŅÐĩŅКÐūÐģÐū ŅÐūŅŅÐūŅÐ―ÐļŅ Ðļ ŅÐĩÐķÐļОÐūÐē ŅКŅÐŋÐŧŅаŅаŅÐļÐļ ÐŧÐūКÐūОÐūŅÐļÐēÐūÐē (ÐÐĄÐÐĒ), Ðē заÐīаŅÐļ КÐūŅÐūŅÐūÐđ ÐēŅ ÐūÐīŅŅ ÐīÐēÐĩ ÐūŅÐ―ÐūÐēÐ―ŅÐĩ ŅŅÐ―ÐšŅÐļÐļ: ÂŦÐĢÐŋŅаÐēÐŧÐĩÐ―ÐļÐĩ ÐļÐ―ŅÐļÐīÐĩÐ―ŅаОÐļÂŧ Ðļ ÂŦÐĢÐŋŅаÐēÐŧÐĩÐ―ÐļÐĩ ÐŋŅÐūÐąÐŧÐĩОаОÐļÂŧ.
ÂŦÐĢÐŋŅаÐēÐŧÐĩÐ―ÐļÐĩ ÐļÐ―ŅÐļÐīÐĩÐ―ŅаОÐļÂŧ ÐŋŅÐĩÐīÐŋÐūÐŧаÐģаÐĩŅ ŅÐļКŅаŅÐļŅ, ŅŅŅŅÐ°Ð―ÐĩÐ―ÐļÐĩ Ðļ ŅÐ°Ð·ÐąÐūŅ КаÐķÐīÐūÐģÐū ÐļÐ―ŅÐļÐīÐĩÐ―Ņа Ņ ÐŧÐūКÐūОÐūŅÐļÐēÐūО: ÐūŅКаз, ÐŋŅÐĩÐīÐūŅÐšÐ°Ð·Ð―ÐūÐĩ ŅÐūŅŅÐūŅÐ―ÐļÐĩ, заОÐĩŅÐ°Ð―ÐļŅ ОаŅÐļÐ―ÐļŅŅÐūÐē, Ð―Ð°ŅŅŅÐĩÐ―ÐļŅ ŅÐĩÐķÐļОÐūÐē ŅКŅÐŋÐŧŅаŅаŅÐļÐļ Ðļ ÐīŅ. Ðа ŅŅÐūО ŅŅаÐŋÐĩ ÐŋŅÐūÐļŅŅ ÐūÐīÐļŅ Ð―Ð°ÐšÐūÐŋÐŧÐĩÐ―ÐļÐĩ ŅŅаŅÐļŅŅÐļКÐļ, Ðē ŅÐūО ŅÐļŅÐŧÐĩ ÐŋÐū ÐīÐ°Ð―Ð―ŅО ÐąÐūŅŅÐūÐēŅŅ ОÐļКŅÐūÐŋŅÐūŅÐĩŅŅÐūŅÐ―ŅŅ ŅÐļŅŅÐĩО ŅÐŋŅаÐēÐŧÐĩÐ―ÐļŅ (ÐÐĄÐĢ).
ÂŦÐĢÐŋŅаÐēÐŧÐĩÐ―ÐļÐĩ ÐŋŅÐūÐąÐŧÐĩОаОÐļÂŧ ÐŋŅÐĩÐīÐŋÐūÐŧаÐģаÐĩŅ Ð°Ð―Ð°ÐŧÐļз ÐīÐ°Ð―Ð―ŅŅ ÐūÐą ÐļÐ―ŅÐļÐīÐĩÐ―ŅаŅ , ÐŋÐūÐļŅК Ðļ ŅŅŅŅÐ°Ð―ÐĩÐ―ÐļÐĩ ÐŋÐĩŅÐēÐūÐŋŅÐļŅÐļÐ― ÐļÐ―ŅÐļÐīÐĩÐ―ŅÐūÐē. Ðа ŅŅÐūО ŅŅаÐŋÐĩ Ð―ÐĩÐūÐąŅ ÐūÐīÐļОÐū ÐļŅÐŋÐūÐŧŅзÐūÐēаŅŅ ÐŋŅÐĩÐīÐŧаÐģаÐĩОŅŅ ОÐĩŅÐūÐīÐļКŅ ŅаŅŅÐĩŅа ŅÐļŅКÐūÐē. ÐÐŧŅ ŅŅÐūÐģÐū ŅÐŧÐĩÐīŅÐĩŅ ŅÐĩаÐŧÐļзÐūÐēаŅŅ ÐļÐ―ŅÐĩŅаКŅÐļÐēÐ―ŅŅ ŅŅÐ―ÐšŅÐļÐūÐ―Ð°ÐŧŅÐ―ÐūŅŅŅ Ð°Ð―Ð°ÐŧÐļза ÐīÐ°Ð―Ð―ŅŅ Ņ ÐēŅŅÐļŅÐŧÐĩÐ―ÐļÐĩО ŅÐļŅКа Ð―Ð°ŅŅŅÐŋÐŧÐĩÐ―ÐļŅ ÐūŅКаза R Ņ ÐļŅÐŋÐūÐŧŅзÐūÐēÐ°Ð―ÐļÐĩО ŅÐĩÐūŅÐļÐļ Ð―ÐĩŅÐĩŅКÐļŅ ÐžÐ―ÐūÐķÐĩŅŅÐē: ÐļÐ―ŅÐūŅОаŅÐļÐūÐ―Ð―Ð°Ņ ŅÐļŅŅÐĩОа ŅаОа ÐŋÐĩŅÐļÐūÐīÐļŅÐĩŅКÐļ ÐīÐūÐŧÐķÐ―Ð° ŅаŅŅŅÐļŅŅÐēаŅŅ ŅÐļŅКÐļ Ðļ, Ðē ŅÐŧŅŅаÐĩ ÐļŅ ÐēÐūÐ·Ð―ÐļÐšÐ―ÐūÐēÐĩÐ―ÐļŅ, ŅÐūÐūÐąŅаŅŅ ÐūÐą ŅŅÐūО ÐūŅÐēÐĩŅŅŅÐēÐĩÐ―Ð―ŅО ŅÐ°ÐąÐūŅÐ―ÐļКаО (ÐēŅÐēÐūÐī ŅÐūÐūÐąŅÐĩÐ―ÐļÐđ Ð―Ð° ŅКŅÐ°Ð―, аÐēŅÐūОаŅÐļŅÐĩŅКаŅ ŅаŅŅŅÐŧКа ŅÐŧÐĩКŅŅÐūÐ―Ð―ŅŅ ÐŋÐļŅÐĩО Ðļ SMS-ŅÐūÐūÐąŅÐĩÐ―ÐļÐđ Ðļ ÐīŅ.).
ÐаÐŧŅÐ―ÐĩÐđŅÐļÐĩ ÐļŅŅÐŧÐĩÐīÐūÐēÐ°Ð―ÐļŅ аÐēŅÐūŅÐūÐē ÐąŅÐīŅŅ Ð―Ð°ÐŋŅаÐēÐŧÐĩÐ―Ņ Ð―Ð° ŅазŅÐ°ÐąÐūŅКŅ аÐēŅÐūОаŅÐļзÐļŅÐūÐēÐ°Ð―Ð―ÐūÐđ ŅÐĩŅ Ð―ÐūÐŧÐūÐģÐļÐļ Ð°Ð―Ð°ÐŧÐļза ÐīÐ°Ð―Ð―ŅŅ ÐąÐūŅŅÐūÐēŅŅ ОÐļКŅÐūÐŋŅÐūŅÐĩŅŅÐūŅÐ―ŅŅ ŅÐļŅŅÐĩО ŅÐŋŅаÐēÐŧÐĩÐ―ÐļŅ Ðļ ÐļÐ―ŅÐūŅОаŅÐļÐūÐ―Ð―ŅŅ ŅÐļŅŅÐĩО ÐķÐĩÐŧÐĩÐ·Ð―ÐūÐīÐūŅÐūÐķÐ―ÐūÐģÐū ŅŅÐ°Ð―ŅÐŋÐūŅŅа Ņ ÐļŅÐŋÐūÐŧŅзÐūÐēÐ°Ð―ÐļÐĩО ОÐĩŅÐūÐīÐūÐē ŅÐĩÐūŅÐļÐđ Ð―ÐĩŅÐĩŅКÐļŅ ÐžÐ―ÐūÐķÐĩŅŅÐē, ŅŅаŅÐļŅŅÐļКÐļ Ðļ Ð―Ð°ÐīÐĩÐķÐ―ÐūŅŅÐļ. Ð ÐĩзŅÐŧŅŅаŅÐūО ÐīÐūÐŧÐķÐ―Ðū ŅŅаŅŅ ŅÐūзÐīÐ°Ð―ÐļÐĩ ŅÐļŅŅÐĩОŅ ÐŋÐūÐīÐīÐĩŅÐķКÐļ ÐŋŅÐļÐ―ŅŅÐļŅ ŅÐĩŅÐĩÐ―ÐļÐđ Ņ ŅŅÐĩŅÐūО ÐūÐķÐļÐīаÐĩОŅŅ ŅÐļŅКÐūÐē Ðē ÐÐĄÐÐĒ ÐÐÐ ÂŦÐÐūКÐūОÐūŅÐļÐēÐ―ŅÐĩ ŅÐĩŅ Ð―ÐūÐŧÐūÐģÐļÐļÂŧ.
ÐŅÐļОÐĩŅÐ°Ð―ÐļÐĩ: Ðē ŅŅаŅŅÐĩ Ð―Ðĩ ŅаŅŅОÐūŅŅÐĩÐ― ÐŋÐūŅŅÐīÐūК ÐūÐŋŅÐĩÐīÐĩÐŧÐĩÐ―ÐļŅ ŅŅÐ―ÐšŅÐļÐđ ÐŋŅÐļÐ―Ð°ÐīÐŧÐĩÐķÐ―ÐūŅŅÐļ \iA(x) â ÐīÐļаÐŋазÐūÐ―Ņ Ðļ ÐŧÐļÐ―ÐĩÐđÐ―ÐūŅŅŅ ÐŋÐĩŅÐĩŅ ÐūÐīа ÐūŅ 0 ÐīÐū 100 % ÐąŅÐŧÐļ ÐēзŅŅŅ ŅОÐūзŅÐļŅÐĩÐŧŅÐ―Ðū Ðļз ŅÐūÐąŅŅÐēÐĩÐ―Ð―ÐūÐģÐū ÐūÐŋŅŅа. ÐÐŧŅ ÐļŅ ŅÐūŅÐ―ÐūÐģÐū ŅаŅŅÐĩŅа ŅÐŧÐĩÐīŅÐĩŅ ÐļŅÐŋÐūÐŧŅзÐūÐēаŅŅ ОÐĩŅÐūÐī ŅКŅÐŋÐĩŅŅÐ―ÐūÐđ ÐūŅÐĩÐ―ÐšÐļ (Ð―Ð°ÐŋŅÐļОÐĩŅ, ОÐĩŅÐūÐī ÐÐĩÐŧŅŅÐļ), ŅÐĩÐūŅÐļŅ ŅŅÐģÐļ ÐŋÐūÐĩзÐīÐūÐē, ŅŅаŅÐļŅŅÐļŅÐĩŅКŅŅ ÐūÐąŅÐ°ÐąÐūŅКŅ ÐīÐ°Ð―Ð―ŅŅ Ðļ ÐīŅŅÐģÐļÐĩ ОÐĩŅÐūÐīŅ.
ÐŋŅÐūŅÐĩŅŅÐūŅ Ð.Ð. ÐÐÐÐÐ,
аŅÐŋÐļŅÐ°Ð―Ņ ÐÐÐÐĒа
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414